BOJ 18189 참 어려운 문제

문제 링크

문제 설명

$i$번 정점의 색이 $A_i$인 크기가 $N$인 트리가 주어질 때,

색깔이 같은 두 정점을 고르면, 이 둘은 항상 조상-자식 관계가 아니다

의 조건을 만족하는 루트가 될 수 있는 정점을 모두 찾아라.

풀이

$r$을 루트로 하는 트리에서, 모든 정점 $u$에 대해 색이 $A_u$인 정점이 $u$의 서브트리에 하나만 있다면 $r$은 루트가 될 수 있다.

오일러 투어 테크닉을 사용하여 서브트리를 연속한 구간으로 바꿔서 이 조건을 빠르게 확인할 수 있다.

예제 1번

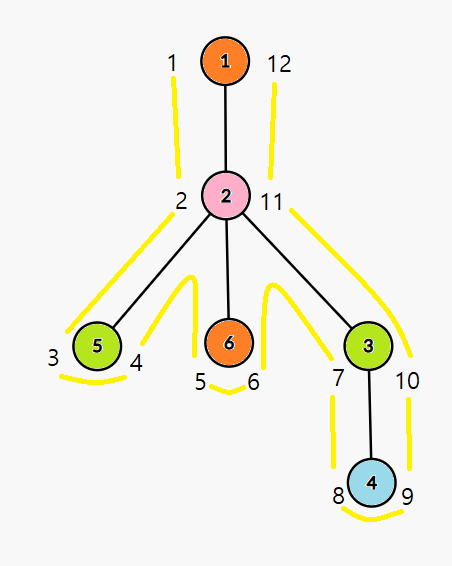
$u$에 들어오는 시간을 $in_u$, 나가는 시간을 $out_u$라고 했을 때, $in_u < in_v < out_v < out_u$인 $v$는 $u$의 서브트리에 속한다.

$A_u=c$인 $u$에 대해 $(in_u, out_u)$을 $time_c$ 리스트에 저장하면, 특정 시간 구간에 색이 $c$인 정점이 몇 개나 있는지 알 수 있다.

서브트리를 이용하기 위해 임의의 정점(보통 1번 정점)을 루트로 삼는다.

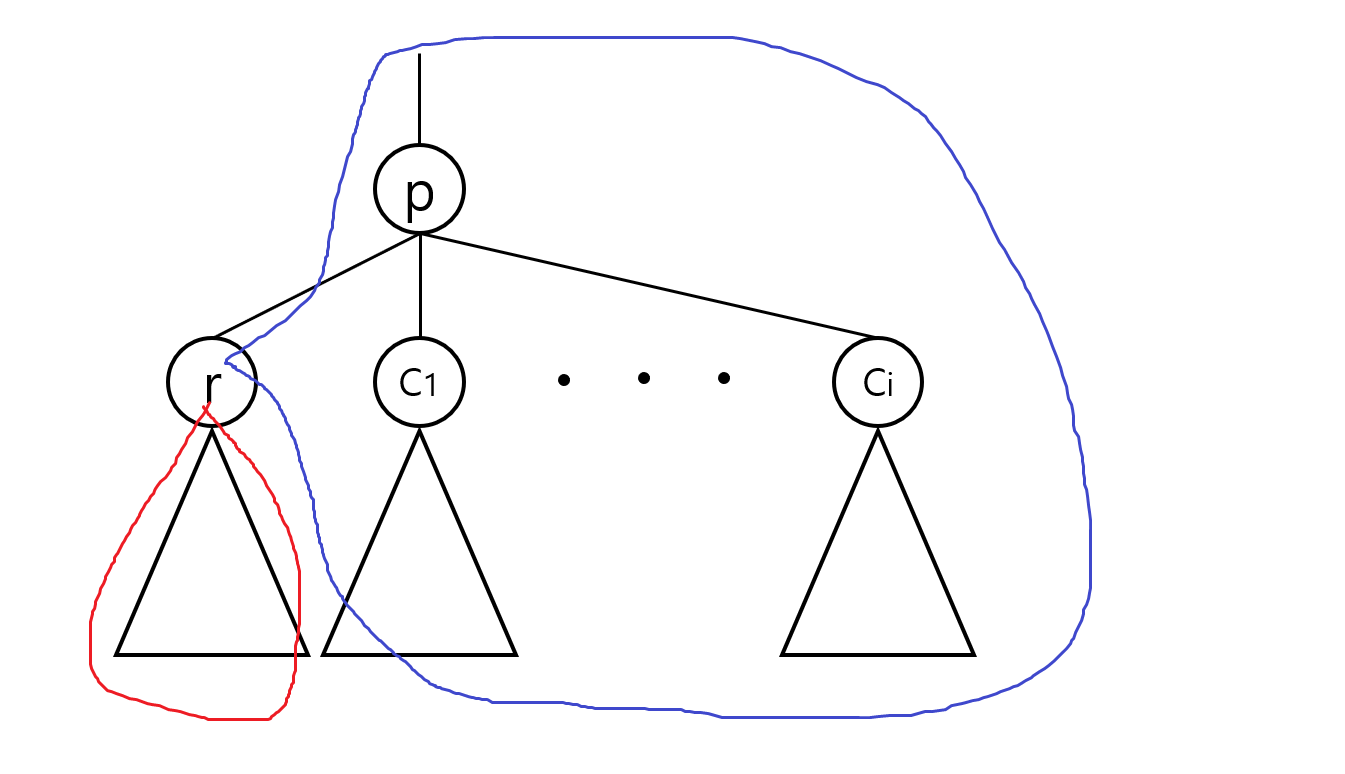
빨간 트리는 $r$의 서브트리이고, 파란 트리는 $r$의 서브트리에 속하지 않은 노드들과 $r$을 가지고 구성한 트리이다.

$r$을 루트로 하는 트리가 가능할지 생각해보자.

빨간 트리와 파란 트리에서 정점을 하나씩 뽑으면 그 둘은 서로 조상-자식 관계가 아니므로, 빨간 트리와 파란 트리 각각에서 $r$이 루트가 될 수 있다면, $r$은 전체 트리에서도 루트가 될 수 있다.

$r$이 빨간 트리에서 루트가 될 수 있는지 여부를 $D_r$, 파란 트리에서 루트가 될 수 있는지 여부를 $P_r$라고 하자.

다음 조건을 만족할 때만 $D_r = \text{True}$이다.

$D_x = \text{True}$ for all $Parent_x = r$
$r$의 서브트리에 색이 $A_r$인 정점이 $r$밖에 없다

다음 조건을 만족할 때만 $P_r$은 $\text{True}$이다.

$p$의 자식이 $r, c_1, \cdots, c_i$일 때,

$P_p = D_{c_1} = D_{c_2} = \cdots = D_{c_i} = \text{True}$
$r$의 서브트리 바깥에 색이 $A_r$인 정점이 없다
$c_1, c_2, \cdots, c_i$의 서브트리 각각에 색이 $A_p$인 정점이 없다

$D_u = P_u = \text{True}$인 $u$는 루트가 될 수 있다.

코드

#include <bits/stdc++.h>
#define all(v) v.begin(), v.end()
#define eb emplace_back
#define time _time
using namespace std;
typedef long long ll;

const int maxn = 250010;

int n, a[maxn], lv[maxn], pa[maxn];
int time, in[maxn], out[maxn];
vector<int> o, adj[maxn], ch[maxn], idx[maxn];
int d[maxn], p[maxn];
ll a1 = 0, a2 = 0, a3 = 0;

void dfs(int now, int prev) {
    ++time;
    in[now] = time;
    idx[a[now]].eb(time);
    for(auto nxt : adj[now]) if(nxt != prev) {
        lv[nxt] = lv[now] + 1;
        pa[nxt] = now;
        ch[now].eb(nxt);
        dfs(nxt, now);
    }
    ++time;
    out[now] = time;
    idx[a[now]].eb(time);
}

void solve(int now) {
    int dcnt = 0;
    for(auto nxt : ch[now]) dcnt += d[nxt];

    int vcnt = lower_bound(all(idx[a[now]]), out[now]) - lower_bound(all(idx[a[now]]), in[now]) + 1;
    for(auto nxt : ch[now]) {
        p[nxt] &= p[now];
        p[nxt] &= (dcnt - d[nxt] == ch[now].size() - 1);

        int ucnt = lower_bound(all(idx[a[now]]), out[nxt] + 1) - lower_bound(all(idx[a[now]]), in[nxt]);
        p[nxt] &= (ucnt == vcnt - 2);
    }

    for(auto nxt : ch[now]) solve(nxt);
}

int main(void) {
    ios_base::sync_with_stdio(0);   cin.tie(0);
    cin >> n;
    for(int i = 1; i <= n; ++i) cin >> a[i];
    for(int i = 1; i <= n - 1; ++i) {
        int u, v;   cin >> u >> v;
        adj[u].eb(v);
        adj[v].eb(u);
    }
    dfs(1, -1);
    for(int i = 0; i <= n; ++i) d[i] = p[i] = 1;

    for(int i = 1; i <= n; ++i) {
        int cnt = lower_bound(all(idx[a[i]]), out[i]) - lower_bound(all(idx[a[i]]), in[i]) + 1;
        if(cnt > 2)                 d[i] = 0;
        if(idx[a[i]].size() != cnt) p[i] = 0;
    }

    for(int i = 1; i <= n; ++i) o.eb(i);
    sort(all(o), [&](int l, int r) { return lv[l] > lv[r]; });
    for(auto v : o) for(auto c : ch[v]) d[v] &= d[c];

    solve(1);

    for(int i = 1; i <= n; ++i) if(d[i] && p[i]) {
        a1 += 1;
        a2 += i;
        a3 += 1LL * i * i;
    }
    cout << a1 << '\n' << a2 << '\n' << a3 << '\n';
    return 0;
}